PROBABILITÉ SUBJECTIVE

PROBABILITÉ SUBJECTIVE

Utilisée parfois par les mathématiciens pour désigner la probabilité «bayésienne» (cf. calcul des PROBABILITÉS), l’expression de probabilité subjective comporte en elle-même une ambiguïté. Elle désigne en effet soit la logique propre de la croyance partiale (en d’autres termes, une théorie normative de la probabilité dans laquelle l’ensemble des jugements portés par un individu hypothétique découle nécessairement des suppositions auxquelles il se livre librement dans des conditions d’incertitude), soit la classe d’estimations, de jugements, de croyances et d’inférences qui guident les individus sans référence obligée à la rigueur et à la cohérence logiques. On n’envisagera ici que la seconde acception, laquelle correspond à l’usage non normatif et recouvre ce que l’on appelle fréquemment la «probabilité psychologique».

En ce sens, la probabilité subjective ne saurait être définie comme un type particulier de mesure. Il s’agit plutôt d’un domaine de recherche qui recouvre une grande variété d’opérations mentales accomplies dans des conditions d’information incomplète et qui, de ce fait même, sont caractérisées par un certain degré d’incertitude subjective. Ainsi définie, la probabilité subjective est indépendante de toute hypothèse quant à la rationalité de l’individu considéré.

Il est alors nécessaire de disposer de plusieurs sortes de mesures dont certaines sont fondées sur des interprétations non psychologiques de la probabilité. Ainsi, en matière de probabilité classique , on admet qu’il existe une concordance entre les résultats d’événements définis mathématiquement (a priori) et des événements physiques répétables, l’exemple le plus courant étant la concordance entre la fréquence observée de pile et de face dans un jeu de pile ou face, et la fréquence attendue (espérance mathématique), qui suppose une probabilité initiale de 0,5 pour pile comme pour face. La contrepartie subjective de cette situation est définie par la concordance entre l’estimation de la fréquence par un sujet et la fréquence théorique calculée. L’opposition entre l’interprétation «fréquentiste» et sa contrepartie psychologique peut être mise en évidence en montrant la différence entre une extrapolation subjective et une extrapolation statistique, par exemple à partir du taux de la mortalité infantile au cours d’une période définie. Toutes les interprétations normatives qu’on utilise dans les inférences statistiques et dans la décision comportent aussi une contrepartie psychologique.

Une mesure particulière de la probabilité subjective peut être faite en évaluant la quantité d’information dont un individu estime devoir disposer pour sortir de son incertitude. En général, lorsqu’il ne dispose d’aucune information au sujet d’un événement particulier, il peut déterminer son jugement en se référant au «principe d’indifférence». Ce principe, introduit par James Bernoulli sous le nom de «principe de raison insuffisante», énonce que, si l’on n’a aucune raison connue de prévoir une éventualité plutôt que telle ou telle autre, la même probabilité doit être attribuée à chacune d’elles. Dans des situations expérimentales de cette nature, les sujets ont en effet tendance à attribuer des probabilités subjectives égales aux différents résultats possibles d’un événement. Puis, à mesure que l’information devient disponible et paraît acceptable au sujet, son incertitude se réduit progressivement. On peut, d’autre part, évaluer son incertitude initiale, dans certaines conditions, par le nombre de questions disjonctives (oui-non) dont il estime avoir besoin pour l’écarter. Lorsque le sujet a répondu à la première question oui-non, son incertitude résiduelle peut de nouveau être mesurée par le nombre de questions binaires qu’il estime devoir encore poser, et ainsi de suite. Cette réduction graduelle de l’incertitude se traduit par un gain d’information subjective qui, dans ce cas, peut être exprimée en bits subjectifs. Dans d’autres circonstances, la probabilité subjective peut être évaluée indirectement par le temps que prend un sujet à répondre «oui» ou «non» à la question: «Réussirez-vous cette tâche ou non?» Pour arriver à une mesure de cette nature, on établit, pour un groupe de sujets, la fréquence relative de succès 祥^s qui est attendue pour n essais dans une tâche donnée, celle-ci étant présentée à divers niveaux de difficulté, de manière à couvrir l’intervalle de 祥^s de 0 à 1. On établit ensuite, pour un groupe équivalent, les temps de décision oui-non pour les mêmes niveaux de difficulté. Les résultats expérimentaux indiquent que, dans certaines conditions, le temps de décision binaire augmente de 1 à 2 secondes lorsque 祥^s tend vers 0,5. La distribution des temps de décision en fonction de la difficulté présente une allure symétrique autour du maximum observé pour 祥^s = 0,5. Les deux moitiés de la distribution peuvent être distinguées par le fait que «oui» indique une expectation de succès élevée, tandis que «non» indique une expectation faible.

1. La notion de chance

Les expressions servant à désigner la probabilité subjective recourent fréquemment à l’idée de «chance», celle-ci pouvant être définie comme la possibilité d’obtenir un gain ou de subir une perte. Du point de vue objectif (comme probabilité statistique p ) aussi bien que du point de vue subjectif (comme probabilité 祥^c ), la chance peut varier en grandeur et être relativement élevée ou relativement faible. On peut alors poser la question générale suivante: combien de chances relativement faibles (p = 0,01, par exemple) sont subjectivement équivalentes à une chance unique plus grande (p = 0,1, par exemple) de gagner un prix donné? Une telle question, qui peut donner lieu à une étude expérimentale, est un modèle de nombreuses situations de la vie courante et de la vie professionnelle dans lesquelles, pour la poursuite d’un but dont l’utilité est supposée constante, plusieurs possibilités limitées doivent être pesées et comparées à une possibilité unique plus importante. Un général peut être amené à choisir entre plusieurs petites batailles, présentant chacune une chance de succès relativement faible, et une seule bataille de grande envergure offrant des chances de succès plus étendues. Un chirurgien peut avoir à choisir entre plusieurs opérations mineures, dont les chances de succès sont faibles, et une seule opération plus importante, mais ayant plus de chances de réussir. De même, un gouvernement peut être amené à choisir entre toute une série de réformes secondaires et une réforme unique et fondamentale. Les résultats des recherches expérimentales semblent montrer que la majorité des sujets (60 p. 100 au moins de la population adulte, semble-t-il) ont tendance soit à surestimer, soit à sous-estimer, par rapport à sa valeur mathématique, une chance relativement petite. Les conditions dans lesquelles ces surestimations et ces sous-estimations se produisent sont complexes et un important travail doit encore être accompli pour dégager les hypothèses les plus plausibles permettant d’expliquer ces phénomènes. Un problème fondamental se pose ici concernant la manière dont un sujet transmet l’information qui lui a été fournie. Comment et pourquoi interprète-t-il dans tel sens particulier les faits qui lui sont présentés dans l’expérience à laquelle on le soumet? De toute évidence, celui qui a tendance à surestimer ne maximalise pas p , mais il se peut qu’il maximalise 祥^c (et donc sa probabilité subjective de gagner un prix). Il est également possible qu’il maximalise l’utilité subjective du prix lui-même. Il n’est pas non plus exclu qu’il maximalise l’utilité du jeu en tant que jeu, en ce sens qu’il peut être plus excitant de miser sur deux petites chances que sur une chance unique plus grande. Un sujet porté à sous-estimer peut au contraire préférer une satisfaction de jeu unique mais puissante. Il semble qu’il y ait une interaction entre 祥^c , la valeur du prix espéré (utilité) et l’excitation liée au jeu lui-même.

2. La «prise de risque»

Sous la forme la plus simple, le risque désigne le niveau d’incertitude subjective à partir duquel un individu est prêt à s’engager dans une action particulière. De deux sujets qui sont prêts à s’engager dans l’action, celui qui pense qu’il a 5 chances sur 10 de succès ( 祥 = 0,5) prend un risque plus grand que celui qui pense avoir 7 chances sur 10 de succès ( 祥 = 0,7). Ainsi donc, dans ce cas particulier de probabilité subjective, celui qui prend un risque ne procède pas seulement à une estimation ou à un jugement, mais passe effectivement à l’action, par exemple en investissant une somme d’argent, en faisant un pari ou en effectuant une manœuvre particulière avec sa voiture sur la route. Selon les circonstances, différentes échelles peuvent être utilisées pour mesurer l’incertitude. On peut employer une échelle de 祥 allant de 0 à n , dans laquelle les nombres de 0 à n correspondent aux succès attendus par le sujet au cours de n essais. Cette échelle peut alors être convertie en une échelle 祥 allant de 0 à 1. L’étendue de l’échelle peut aussi aller de 祥 = 0,5 (incertitude maximale) à 1 (certitude maximale). On peut encore utiliser une échelle d’estimation à n valeurs, dans laquelle chaque point correspond à la confiance attribuée par le sujet à un certain résultat qui a eu lieu ou qui doit encore se produire.

Dans certaines situations, une telle estimation constitue une probabilité subjective du deuxième ordre. On dira que l’estimation du premier ordre, 祥¹, représente l’estimation du nombre de performances réussies dans une tâche donnée, tandis que l’estimation du deuxième ordre 祥² exprime la confiance de l’individu dans sa première estimation; elle indique, pour ainsi dire, le degré de certitude que possède le sujet de sa propre certitude. Il est possible, en principe, d’obtenir des valeurs de 祥 d’un ordre encore supérieur, mais leur mesure ne présente plus une fidélité suffisante. On peut admettre que toute affirmation, toute estimation ou tout jugement de la catégorie 祥¹ émis par un sujet implique tacitement l’existence d’une certaine valeur de 祥².

Il importe de distinguer le risque du danger. Dans de nombreuses situations, il est possible de mesurer le risque d’après la fréquence qu’un sujet estime avoir de tomber au-dessous d’un critère donné de réussite, tandis que le danger correspondant est mesuré par la fréquence effective selon laquelle le sujet tombe au-dessous de ce critère, cette fréquence étant établie à partir d’un échantillon représentatif d’occurrences. On peut considérer que le risque et le danger sont fonction l’un et l’autre à la fois de l’habileté de l’individu et du jugement qu’il porte sur cette habileté même.

La proportion de réussites qu’un individu espère atteindre dans une tâche donnée semble être effectivement liée à la difficulté de celle-ci. Considérons une tâche susceptible d’être graduée quant à sa difficulté et calibrée séparément pour chaque individu à partir de ses performances actuelles dans une série d’épreuves. En général, les sujets ne sont pas uniformément «réalistes» dans l’estimation de leurs réussites. Une série d’expériences montre que le réalisme du jugement est maximal à un niveau de réussite de 30 p. 100. Lorsque le taux de réussite est plus bas, les estimations sont exagérées et, lorsqu’il est supérieur, les estimations ont tendance à minimiser la performance actuelle. Dans les travaux et activités qui présentent un danger, il est possible de réduire la probabilité de dommage ou de catastrophe en optimalisant le rapport entre risque et danger.

Mais il reste un problème non résolu, celui de savoir si la tendance à prendre des risques est soit un facteur général qui intervient de façon plus ou moins constante dans toutes les actions d’un individu, soit un facteur de groupe susceptible d’intervenir dans un sous-ensemble homogène d’actions, mais pas nécessairement dans d’autres sous-ensembles, soit encore un facteur spécifique propre à chaque situation particulière.

La troisième hypothèse n’implique pas nécessairement que le comportement humain soit entièrement capricieux (ou «libre»), en ce sens qu’aucune prédiction ne pourrait jamais être faite d’une action à une autre; elle signifie simplement qu’une configuration unique caractérise chaque situation et détermine le degré de risque qu’une personne est prête à assumer.

3. Influence de la croyance à la chance

Un aspect de la probabilité subjective qui joue un rôle important est la croyance à la chance. Ce que nous croyons qui arrivera est fonction de ce que nous pensons qui arrivera si nous avons de la chance ou non. Cette croyance a tendance à s’établir de manière ferme et cohérente. Considérons la question suivante: «Combien de fois pensez-vous effectivement pouvoir enfiler dans le chas d’une aiguille donnée un fil donné pendant une demi-heure?» Le sujet auquel on a posé la question est averti qu’après avoir fourni une estimation réaliste à propos de celle-ci, il aura la possibilité de montrer son habileté pour cette tâche avec des aiguilles de différentes dimensions. On lui demande alors de procéder à quatre ensembles supplémentaires d’estimations en supposant qu’il aura de la chance (c ), qu’il aura beaucoup de chance (C), qu’il aura de la malchance ( 縷 ) ou qu’il aura beaucoup de malchance (face="EU Upmacr" 綠). Les estimations varient, bien entendu, selon la tâche considérée, mais un type de résultat (pour un sujet hypothétique) est exprimé schématiquement par la figure ci-dessus, où r désigne l’estimation réaliste. Pour certaines catégories de tâches, comme les performances athlétiques, les sujets s’attendent généralement à ce que leurs estimations réalistes se confirment en moyenne dans un essai sur six, et à avoir beaucoup de chance ou beaucoup de malchance dans un essai sur quatorze. Ils espèrent en outre que, s’ils ont de la chance, leur performance s’améliore de 6 à 12 p. 100, et, s’ils ont beaucoup de chance, de 12 à 26 p. 100. En cas de malchance, ils s’attendent à ce que leur performance diminue de 15 à 40 p. 100, et, s’ils ont beaucoup de malchance, de 17 à 80 p. 100.

4. Prise de décision dans l’incertitude

L’expression «prise de décision dans l’incertitude» peut désigner soit le processus qui consiste à peser, consciemment et inconsciemment, le pour et le contre de différentes suites d’action possibles, soit l’acte même de décision, soit enfin la décision elle-même, c’est-à-dire le résultat final comme tel. La théorie normative de la prise de décision se réfère principalement au premier sens, c’est-à-dire à l’évaluation des avantages et des inconvénients de plusieurs actions possibles. On entend généralement par là l’activité par laquelle un individu envisage explicitement les possibilités qui lui sont offertes et assigne à chacune d’elles une probabilité p d’occurrence et une utilité u , cette dernière exprimant la valeur (désirabilité) qu’il lui attribue. Les modèles normatifs admettent, par hypothèse, que l’individu se décide en faveur de la possibilité pour laquelle le produit de p et de u est maximal. Dans les théories descriptives , la mise à l’épreuve de tels modèles – dont certains substituent 祥 à p (probabilité statistique ou a priori) et/ou l’utilité subjective u à l’utilité objective u – a surtout été effectuée dans le domaine économique. Mais les modèles de ce genre ont des applications assez limitées. Les limitations sont principalement imputables, en premier lieu, au fait que certains d’entre eux font l’hypothèse non vérifiée que les sujets expérimentaux disposent d’un inventaire complet des «états de la nature» possibles, ce qui n’est généralement pas le cas; en deuxième lieu, au fait qu’ils supposent que les sujets ordonnent transitivement les résultats possibles et choisissent celui pour lequel la somme des produits de 祥 et de u est maximale. Enfin, des modèles omettent plusieurs facteurs qui peuvent se révéler importants: ainsi, la variance des différents paris, l’incertitude subjective attribuée à un résultat particulier, l’effet de la croyance à la chance, le degré de croyance à son habileté propre plutôt qu’à la chance, l’utilité du jeu comme tel, les grandeurs relatives de l’enjeu et du prix.

Décisions de jeu

L’influence exercée par la probabilité subjective dans les décisions de jeu apparaît clairement dans des situations de choix équiprobable, par exemple lorsque la probabilité statistique a priori de gagner un prix est identique dans deux loteries et que le sujet ne peut prendre un billet qu’à l’une ou à l’autre. Un éventail étendu de situations de loterie de cette espèce peut être représenté de façon commode par la notation suivante:

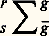dans laquelle représente le nombre total d’extractions effectuées par un sujet à partir d’une ou de plusieurs sources données; s , le nombre de sources identiques pour lesquelles les extractions sont permises et entre lesquelles est également divisé; g , le nombre de billets gagnants; 凜 , le nombre de billets non gagnants; r indique que chaque billet extrait d’une source est remis en jeu aléatoirement (à la même source) avant l’extraction suivante. L’absence de r signifie que la remise en jeu n’a pas lieu.

Considérons, à titre d’illustration, les trois types de choix binaires offerts à un sujet et dans lesquels la probabilité d’extraire le billet gagnant est respectivement de 0,1, de 0,5 et de 0,9:

formule dans laquelle g , 凜 prennent, selon le cas, les couples de valeurs 1: 9; 2: 18 et 5: 45 (la notation 1: 9 signifie une chance contre neuf, donc une chance sur dix);

où g , 凜 prennent, selon le cas, les valeurs

5: 5; 10: 10 et 25: 25:

où g , 凜 prennent, selon le cas, les valeurs pairées 9: 1; 18: 2 et 45: 5.

On constate que dans de telles situations, si le prix est constant, la plupart des sujets préfèrent prendre un billet à la plus grande de deux loteries lorsque p = 0,1 et à la plus petite lorsque p = 0,5 ou 0,9.

Prises de décision professionnelles

L’évaluation des incertitudes personnelles, qui intervient dans la probabilité subjective, affecte la prise de décision professionnelle au même titre que les innombrables décisions de nature économique, éthique, sociale ou esthétique imposées par la vie quotidienne. Les domaines médical et juridique fournissent ici des exemples frappants. Dans la pratique clinique, le médecin assigne «intuitivement» des probabilités à divers diagnostics possibles. Il peut également leur assigner des probabilités subjectives conditionnelles 祥 (S/M); étant donné que le patient souffre d’une maladie M, quelle est la vraisemblance de l’apparition ultérieure de certains symptômes S? Toutefois, c’est l’opération inverse qui est effectuée le plus fréquemment, c’est-à-dire 祥 (M/S). En d’autres termes, étant donné que le patient présente certains symptômes, quel degré de vraisemblance y a-t-il pour qu’il soit atteint de telle maladie particulière? Si l’on possédait une information statistique, on pourrait appliquer à cette situation la formule de Bayes (qui donne la valeur de la probabilité composée dite «probabilité des causes» ou «probabilité des hypothèses»). Mais une telle information peut faire défaut et, même si elle existe, il est possible que le médecin l’ignore. Il ne connaît donc que les symptômes et c’est sur cette base qu’il doit inférer l’existence de la maladie la plus «probable». Les essais auxquels on procède actuellement pour remplacer le diagnostic médical par le calcul numérique tentent avant tout de remplacer les éléments purement subjectifs par des probabilités établies à partir des dossiers médicaux.

Le domaine juridique fournit de nombreux exemples de situations où le juge autant que les jurés demeurent dans une incertitude considérable, mais où néanmoins doit être rendu un verdict se situant «au-delà du doute raisonnable» ou traduisant l’«intime conviction» des juges. Dans d’autres situations, il existe également une «prépondérance de probabilité» concernant les faits soumis au tribunal. Les recherches montrent que l’interprétation de ces expressions juridiques utilisées par le juge dans les instructions qu’il donne aux jurés (la première et la troisième appartiennent au droit anglais et la deuxième au Code civil) varie considérablement d’une personne à l’autre. Il apparaît qu’en Angleterre un tiers des sujets pris dans un échantillon caractéristique d’adultes interprète le «doute raisonnable» à un niveau de 祥 inférieur à 0,7 et qu’un autre tiers considère qu’une valeur de 祥 égale à 0,9 représente encore un doute trop important.

Décision chez le délinquant

L’état d’esprit d’un délinquant en puissance semble pouvoir parfois être mieux compris si l’on supposait que sa décision est fondée sur son interprétation de l’incertitude de sa prévision. Dans de nombreuses circonstances, le délinquant préfère sans aucun doute l’utilité découlant de l’acte délictueux à l’utilité moindre d’une existence conforme à la loi. Mais, dans d’autres cas, la situation peut être plus complexe: le délinquant pèserait la probabilité d’être malchanceux, et donc de perdre sa liberté de mouvement L – laquelle présente une certaine utilité u –, par rapport à la probabilité de recueillir un butin B d’une certaine importance, ce qui comporte un certain risque d’encourir une pénalisation P. On peut représenter cette situation en disant que le délinquant prend sa décision en évaluant: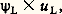

contre:

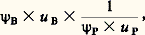ce qui suppose toutefois que le délinquant fasse tacitement le produit de 祥 et de u .

5. Aspects génétiques

Les idées se rapportant au registre de la probabilité subjective ne surgissent pas toutes faites du cerveau de l’adulte, mais connaissent une longue histoire dont les débuts se situent dans la première enfance. Jusqu’à l’adolescence, on constate une régression graduelle des éléments subjectifs et une convergence corrélative vers les interprétations objectives, encore que le subjectif ne perde jamais entièrement ses droits. Cette convergence est imputable partiellement à la maturation et partiellement aux effets de l’apprentissage, ces derniers fournissant une connaissance des résultats et donc un renforcement. Vers l’âge de cinq ans, l’enfant utilise des mots comme «probablement» et d’autres expressions tirées du sous-langage de l’incertitude, pour indiquer, ne fût-ce que de façon ordinale, la probabilité subjective qu’il attribue à une possibilité particulière (par exemple, la possibilité que son jouet se trouve dans telle chambre ou dans telle autre). On peut mettre en évidence à ce propos des stades de développement que servent à illustrer les notions d’indépendance et de distribution.

Indépendance

D’une urne, dont on dit au sujet qu’elle contient des jetons bleus et des jetons jaunes, on extrait l’un après l’autre trois jetons, apparemment au hasard, deux de ceux-ci ayant la même couleur et le troisième l’autre couleur. La tâche du sujet consiste à deviner la couleur du quatrième jeton à extraire. De six à quinze ans, la tendance à prédire, pour le jeton suivant, la couleur non prépondérante diminue de façon régulière, tandis que s’affirme la tendance à déclarer que le quatrième jeton pourrait avoir indifféremment l’une ou l’autre couleur. Autrement dit, dans ces conditions, l’«effet négatif de récence» diminue avec l’âge.

Plus généralement, les enfants de moins de sept ans qui doivent prédire le résultat d’un événement binaire, au cours d’une série d’essais avec connaissance des résultats, ont tendance à prévoir B quand l’événement précédent est A, et réciproquement; lorsqu’ils ne procèdent pas exactement de la sorte, ils se décident dans la plupart des cas en faveur du résultat jusque-là non prépondérant. Le choix de la réponse «opposée» est plus fréquent après une prévision exacte qu’après une réponse erronée. Chez les enfants plus âgés, cette tendance est moins marquée. Au-dessous de dix ans, les enfants distinguent très rarement un événement binaire dont le résultat est indépendant des résultats précédents (comme dans le jeu de pile ou face) d’un événement binaire dont le résultat dépend des résultats précédents à un degré variable (comme la prévision du temps atmosphérique à un moment particulier). La compréhension claire de l’indépendance des événements ou résultats n’apparaît qu’entre douze et quatorze ans.

Distribution

Une expérience caractéristique consiste à montrer à un sujet une urne contenant un nombre non spécifié de jetons bleus (B) et de jetons jaunes (J). La proportion relative des couleurs ne lui est pas fournie. Quatre jetons sont extraits de l’urne et placés dans une coupelle. L’opération est répétée jusqu’à obtenir seize échantillons comprenant chacun quatre jetons. La tâche du sujet consiste à deviner combien des seize coupelles contiennent 0, 1, 2, 3 ou 4 jetons bleus. L’analyse des réponses montre qu’entre dix et quinze ans il existe quatre stades dans le développement de l’idée de distribution. Au premier stade, les sujets assignent simplement des nombres différents aux cinq catégories; au deuxième, c’est le nombre assigné à la catégorie (2 B, 2 J) qui prédomine; au troisième on constate une tendance à assigner des proportions semblables à (1 B, 3 J) et à (1 J, 3 B), d’une part, et à (0 B, 4 J) et à (0 J, 4 B), d’autre part; enfin, au quatrième stade, lequel est atteint aux environs de quatorze ans, la fréquence attribuée à (1 B, 3 J) est plus grande que celle attribuée à (0 B, 4 J); de même, la fréquence attribuée à (3 B, 1 J) est supérieure à celle qui est attribuée à (4 B, 0 J).

Ajoutons, pour conclure, que, si les modèles non normatifs suffisent pour comprendre la probabilité subjective considérée du point de vue psychologique, des éléments normatifs doivent nécessairement intervenir pour atteindre l’optimum de décision et de choix dans des situations pratiques, comme celles que l’on rencontre, par exemple, dans les domaines administratif, économique ou militaire.

Encyclopédie Universelle. 2012.